English
Diophantine equations and elliptic curves
在上一篇 post 中,我们介绍了在椭圆曲线上的 weil pairing 和 tate pairing。在这一篇中我们考虑椭圆曲线在丢番图方程上的一些应用。
问题零
我们在初中数学中学过,直角三角形满足勾股定理,设两个直角边为a b c
a 2 + b 2 = c 2 那么满足三边均为整数的直角三角形有无数个吗?
这便是一个丢番图方程的经典例子。一般而言,丢番图方程(Diophantine equations)是有一个或者几个变量的整系数 方程,它们的求解仅仅在整数范围 内进行。
我们学到的最简单的方程应该是线性丢番图方程,即形如:
a x + b y = c 的方程,其中 a , b , c x , y
当然,上面这道题并不需要用到 elliptic curves 的内容来进行分析(所以才叫“问题零”)。
下面说一下问题零的解答,注意到:
( x 2 − y 2 x 2 + y 2 ) 2 + ( 2 x y x 2 + y 2 ) 2 = 1
这个其实是初中数学老师的某一堂课注意到的。
因此满足三边长度均为整数的直角三角形有无数个,令 x > y > 0 , x , y ∈ Z a = x 2 − y 2 , b = 2 x y , c = x 2 + y 2
例如:
x = 2 , y = 1 → ( 3 , 4 , 5 )
x = 3 , y = 1 → ( 6 , 8 , 10 )
x = 3 , y = 2 → ( 5 , 12 , 13 )
问题一
我们在小学数学时就学过直角三角形的面积为
S = 1 2 a b 那么问题是,可以找到面积S = 5
这道题相当于我们有两个条件的 diophantine equation:
{ a 2 + b 2 = c 2 a b = 10 要求其有理数解。如果我们如法炮制用 x , y a , b
( x 2 − y 2 ) x y = 5 的有理数解,方程的次数变成了4
我们注意到:
( a ± b 2 ) 2 = a 2 ± 2 a b + b 2 4 = ( c 2 ) 2 ± 5
这个是书上说注意到的,这个应该比上一个显然。
因此我们设x = ( c 2 ) 2
只要找到一组解 ( x − 5 , x , x + 5 ) ( a , b , c )
如果 x − 5 , x , x + 5 x 3 − 25 x
E : y 2 = x 3 − 25 x 来寻找里面 non-trivial 的有理点。
找到第一个解
我们首先可以找到三个有理点 ( 0 , 0 ) ( ± 5 , 0 ) 5 − 5
通过简单的搜索,我们可以找到一个非平凡的有理点( − 4 , 6 ) c ( c 2 ) 2 = − 4 c
但我们可以从这个点出发做切线,来与 E
我们尝试做点 ( − 4 , 6 ) E
2 y y ′ = 3 x 2 − 25 y ′ = 3 x 2 − 25 2 y 代入点 ( − 4 , 6 ) y ′ = 23 12
y = 23 12 ( x + 4 ) + 6 将该函数与 E
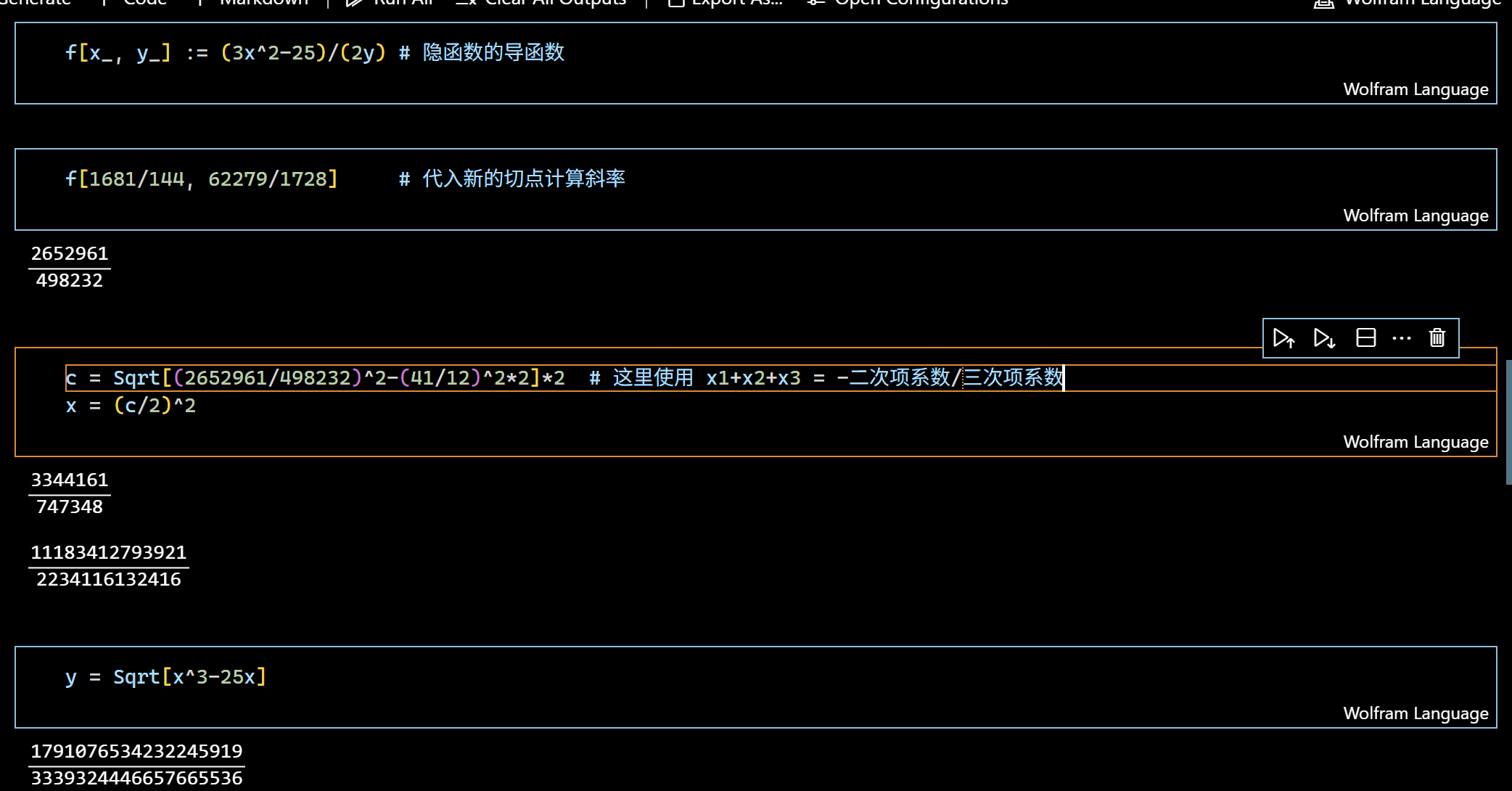
( 23 12 ( x + 4 ) + 6 ) 2 = x 3 − 25 x 展开后可得常数项为 − 41 2 9 x 1 x 2 x 3 = − C = 41 2 9 C E x = − 4 x 1 , 2 = − 4 x 3 = 41 2 9 ÷ ( − 4 ) 2 = ( 41 12 ) 2
我们得到了对应的 x 3 c = 41 6
( a ± b 2 ) 2 = a 2 ± 2 a b + b 2 4 = ( c 2 ) 2 ± 5 因此:
( a ± b 2 ) 2 = ( 41 12 ) 2 ± 5 可以发现 ( 41 12 ) 2 ± 5 a = 20 3 , b = 3 2
综上,我们得到了一个解 ( a , b , c ) = ( 20 3 , 3 2 , 41 6 ) 5
证明解有无穷多个
下一个问题是,存在无数个这样的三元组 ( a , b , c )
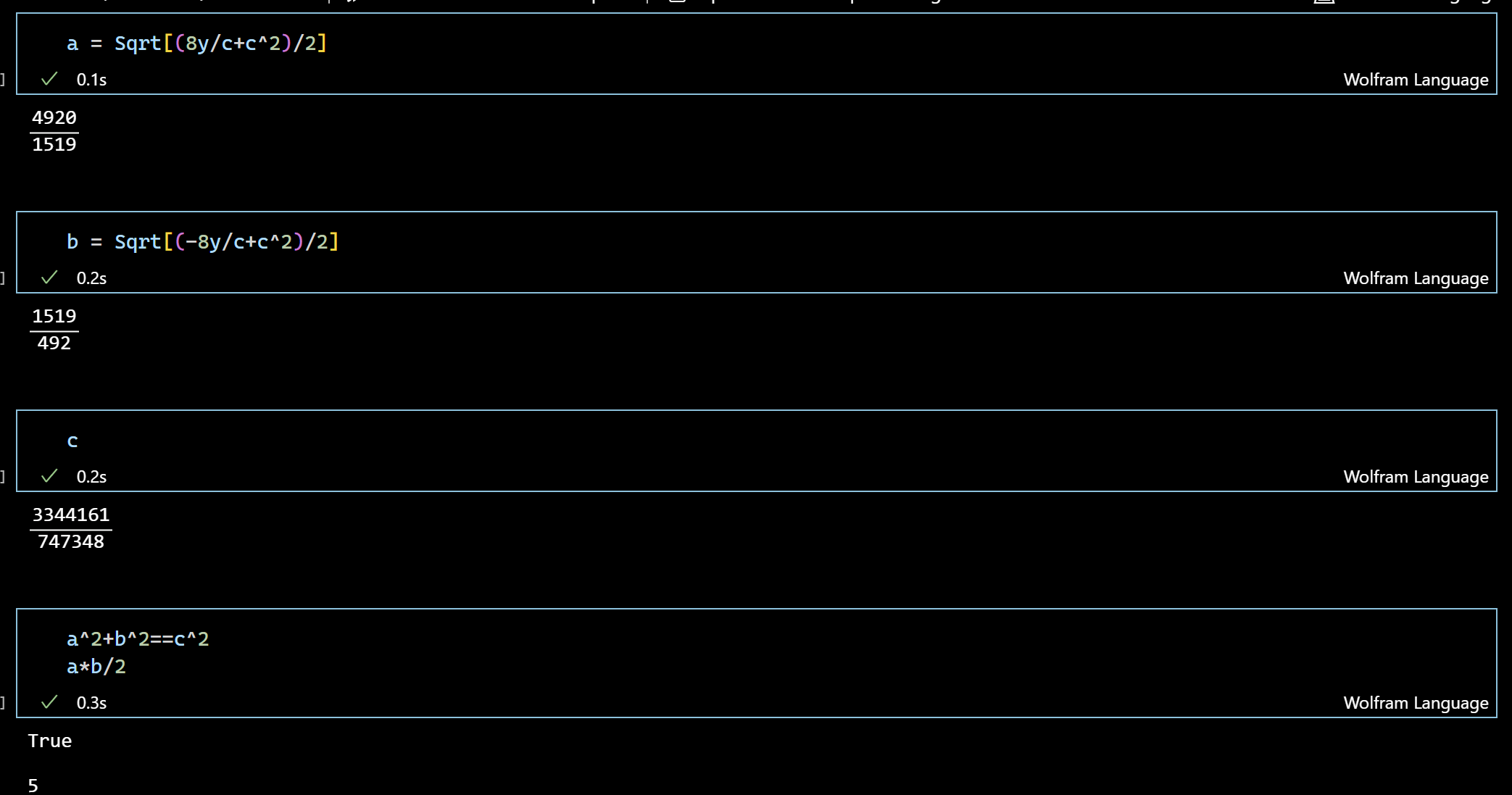
因为 y = ( ( x − 5 ) x ( x + 5 ) ) 1 / 2 = ( a − b ) c ( a + b ) 8 = ( a 2 − b 2 ) c 8 a 2 − b 2 = 8 y / c a 2 + b 2 = c 2 a = ( 8 y / c + c 2 ) / 2 , b = ( − 8 y / c + c 2 ) / 2
因此得到下一个三元组 ( 4920 1519 , 1519 492 , 3344161 747348 ) a , b , c
我们讨论类似这样的一般方程:
E : y 2 = x 3 − n 2 x 中有非平凡有理数点( x 0 , y 0 ) x 0 ≠ 0 , ± n E ( x 1 , y 1 ) x 1 − n , x 1 , x 1 + n
首先我们求出切线方程:
y = ( 3 x 0 2 − n 2 2 y 0 ) ( x − x 0 ) + y 0 根据韦达定理,可得:
x a x b x c = ( y 0 − ( 3 x 0 2 − n 2 ) x 0 2 y 0 ) 2 = ( 2 y 0 2 − 3 x 0 3 + n 2 x 0 2 y 0 ) 2 = ( 2 x 0 3 − 2 n 2 x 0 − 3 x 0 3 + n 2 x 0 2 y 0 ) 2 = ( x 0 3 + n 2 x 0 2 y 0 ) 2 因为 x a , b x 0 x 1 = x c = ( x 0 2 + n 2 2 y 0 ) 2 x 1 c
注意到:
x 1 ± n = ( ( x 0 2 + n 2 ) 2 ± 4 n y 0 2 4 y 0 2 ) = ( x 0 2 ± 2 n x 0 − n 2 2 y 0 ) 2
这个是 deepseek R1 注意到的,我注意力不行(
因此 x 1 ± n
( a ± b 2 ) 2 = ( c 2 ) 2 ± n = x ± n 即 a ± b 2 a , b
我们可以按照这种迭代方法生成x 2 , x 3 , ⋯ a , b , c n E n
问题二
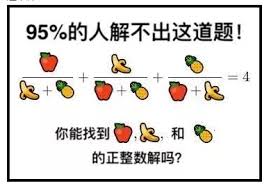
这是我在初中时同学给我的一道钓鱼题:
我当时试了一下,发现这个问题能解决的人数占比应该没有 5%。事后同学告诉了我那三个巨长的答案,于是我意识到了一些数论问题的魅力:
看上去十分简单的问题陈述,其答案和解法却非常复杂。
化为 Weierstrass 形式
首先这个方程是齐次的,这意味着只要我们找到一组解( a , b , c ) t ∈ N + ( t a , t b , t c )
按照问题一的思路,我们首先应该考虑如何将题目所给的方程:
a b + c + b a + c + c a + b = 4 , a , b , c ∈ N + 转化为椭圆曲线的形式——这个可比问题一的难度大多了。
首先尝试通分:
a 3 + b 3 + c 3 − 3 a 2 b − 3 a 2 c − 3 a b 2 − 3 b 2 c − 3 a c 2 − 3 b c 2 − 5 a b c = 0 然后我们需要用a , b , c x , y F
y 2 + a 1 x y + a 3 y = x 3 + a 2 x 2 + a 4 x + a 6 可以通过穷举找到 F P = ( 1 , − 1 , 0 ) P F
{ ∂ F ∂ a = 3 a 2 − 6 a b − 6 a c − 3 b 2 − 3 c 2 − 5 b c ∂ F ∂ b = 3 b 2 − 6 a b − 6 b c − 3 a 2 − 3 c 2 − 5 a c ∂ F ∂ c = 3 c 2 − 6 a c − 6 b c − 3 a 2 − 3 b 2 − 5 a b 然后代入( 1 , − 1 , 0 ) ( 6 , 6 , − 1 ) Z = 6 a + 6 b − c
令Z = 0 c = 6 a + 6 b F F = 91 ( a + b ) 3 P a + b = 0 P 3 参考文献六 ,我们需要找到一个变换矩阵M β
M β = ( Q x P x . Q y P y . Q z P z . ) 是可逆矩阵。一个简单的做法是令点 Q Z ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) ( 0 , 0 , 1 )
例如取M β
M β = ( 1 1 0 0 − 1 0 6 0 1 ) 令a = u + v , b = − v , c = 6 u + w F ( a , b , c ) F ( u , v , w )
91 u 3 + 69 u 2 w − u v w − v 2 w + 15 u w 2 + w 3 = 0 v 2 w + u v w = 91 u 3 + 69 u 2 w + 15 u w 2 + w 3 1 91 v 2 w + 1 91 u v w = u 3 + 69 91 u 2 w + 15 91 u w 2 + 1 91 w 3 令w ′ = w / 91
v 2 w ′ + u v w ′ = u 3 + 69 u 2 w ′ + 1365 u w ′ 2 + 8281 w ′ 3 两边同时除以w ′ 3 X = u / w ′ , Y = v / w ′
Y 2 + X Y = X 3 + 69 X 2 + 1365 X + 8281 这两者便是参考文献六 一开始提到的投影形式和仿射形式。
这个时候我们尝试将 ( u , v , w ) ( a , b , c )
{ u = a + b v = − b w = − 6 a − 6 b + c 然后就能得到 ( X , Y ) ( a , b , c )
{ X = − 91 ( a + b ) 6 a + 6 b − c Y = 91 b 6 a + 6 b − c 同样我们也可以算出其逆变换(这里省略了自由变量k
{ a = − X − Y b = Y c = − 6 X − 91 找到一组正整数解
尝试暴力穷举寻找新的方程的整数解,可以通过脚本枚举 X , Y ∈ [ − 100 , 100 ]
(-39 , 52 )
(-39 , -13 )
(-28 , 63 )
(-28 , -35 )
(-15 , 11 )
(-15 , 4 )
(-14 , 7 )
(-13 , 13 )
(-13 , 0 )
(0 , 91 )
(0 , -91 )
把解带回( a , b , c )
( x, y) = ( - 39 , 52 ) -> ( a, b, c ) = ( - 13 , 52 , 143 ) [ Valid]
( x, y) = ( - 39 , - 13 ) -> ( a, b, c ) = ( 52 , - 13 , 143 ) [ Valid]
( x, y) = ( - 28 , 63 ) -> ( a, b, c ) = ( - 35 , 63 , 77 ) [ Valid]
( x, y) = ( - 28 , - 35 ) -> ( a, b, c ) = ( 63 , - 35 , 77 ) [ Valid]
( x, y) = ( - 15 , 11 ) -> ( a, b, c ) = ( 4 , 11 , - 1 ) [ Valid]
( x, y) = ( - 15 , 4 ) -> ( a, b, c ) = ( 11 , 4 , - 1 ) [ Valid]
其中第五、六行就是参考资料四 中使用的特殊解。
但此时对应的 ( a , b , c ) ( x , y ) = ( − 15 , 4 ) ( a , b , c )
这里的过程就比较简单了,只需暴力循环无脑判断就行。这里我也懒得造轮子,直接让 GPT 写 sagemath 的椭圆曲线库搞定:
E = EllipticCurve(QQ, [1 , 69 , 0 , 1365 , 8281 ])
def compute_abc (x, y ):
a = -x-y
b = y
c = -6 *x-91
return a, b, c
def is_positive_integer (a, b, c ):
return (a > 0 and b > 0 and c > 0 )
def find_positive_abc (P, max_iterations ):
iteration = 1
while iteration < max_iterations:
try :
Q = (iteration * P)
x, y = Q.xy()
except Exception as e:
print (f"Error in point doubling: {e} . Stopping." )
break
a, b, c = compute_abc(x, y)
if is_positive_integer(a, b, c):
print (f"Found positive integer solution when iteration = {iteration} " )
return Q, a, b, c
iteration += 1
print ("No positive integer (a, b, c) found within max iterations." )
return None
point = E([-15 , 4 ])
result = find_positive_abc(point, max_iterations=10 )
if result:
Q, a, b, c = result
print (f"Solution: (a, b, c) = ({a} , {b} , {c} )" )
与参考资料四 相同,当迭代次数 iteration=9 时,输出为:
a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 12568549348783827476450917658335170150704695563440250577574035123362243258771752 b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 12568549348783827476450917658335170150704695563440250577574035123362243258771752 c = 9405501114660716625534518421595417184664937929417781 27028800585432577024141815890005886705385156000813842 同时乘他们最小公倍数即可得到正整数解:
a = 154476802108746166441951315019919837485664325669565431700026634898253202035277999 b = 36875131794129999827197811565225474825492979968971970996283137471637224634055579 c = 4373612677928697257861252602371390152816537558161613618621437993378423467772036 问题三
有好事者在问题二梗图的启发下,把一个看上去更简单的问题搞成了这种人畜无害的形式:
这就是著名的“三立方和问题”,即求:
x 3 + y 3 + z 3 = k 的整数解 ( x , y , z )
而图片中的问题,即 k = 33
由于这个方程不是齐次方程,所以问题二的倍点方法又行不通了。Andrew 发的论文思路是通过降低暴力枚举的时间复杂度(从 O ( N 1 + o ( 1 ) ) O k ( N ( log log N ) ( log log log N ) ) N = 10 16
O ( N 1 + o ( 1 ) ) 首先考虑问题的弱化版——两立方和问题,一个比较简单的结论是对于质数p
x 3 + y 3 = p 有整数解的 p 2 3 n 2 − 3 n + 1
因为 x 3 + y 3 = ( x + y ) ( x 2 − x y + y 2 ) p
x + y = 1 ∨ x 2 − x y + y 2 = 1 先考虑右式,只有x = 1 , y = 1 p 2
再考虑左式,令 y = 1 − x 3 x 2 − 3 x + 1
我们尝试将 p k k = r s r = x y , s = x 2 − x y + y 2 y = r − x
s = 3 x 2 − 3 r x + r 2 是个标准的一元二次方程。则 Δ = ( − 3 r ) 2 − 4 ∗ 3 ∗ ( r 2 − s ) = 12 s − 3 r 2 Δ Δ = t x = ( 3 r + t ) / 6 , y = ( 3 r − t ) / 6 x , y
回到先前的三立方和问题,可以将 z 3
x 3 + y 3 = k − z 3 然后应用之前的两立方和问题判断算法,只需枚举z O ( N 1 + o ( 1 ) )
转化为椭圆曲线
假设 x 3 + y 3 + z 3 = k > 0 , | x | > | y | > | z | ≥ k d = | x + y | z k d
x , y = sgn ( k − z 3 ) 2 ( d ± 4 | k − z 3 | − d 3 3 d ) 这里sgn ( x ) x sgn ( 0 ) = 0 , sgn ( x ) = x | x |
则
Δ = 4 | k − z 3 | − d 3 3 d = ◻ 这里 ◻
3 d ( 4 sgn ( z ) ( z 3 − k ) − d 3 ) = ◻ ∧ z 3 ≡ k mod d 对于给定的搜索范围N N = 10 16 d ∈ [ 0 , ( 2 3 − 1 ) N ] 3 d z ∈ [ − N , N ] z 3 ≡ k mod d ( d , z ) ( x , y , z )
对于指定的整数k E d
E d : Y 2 = X 3 − 2 ( 6 d ) 3 ( d 3 + 4 sgn ( z ) k ) 使得对应的整点恰好是上式的整数解,具体的映射为
{ X = 12 d | z | Y = ( 6 d ) 2 | x − y | 于是这个问题又转化为了在Q
这种代数变换对于较小的 d ( x , y , z ) k
33 , 42 , 114 , 165 , 390 , 579 , 627 , 633 , 732 , 795 , 906 , 921 , 975. Booker 使用了代数软件 Magma 的椭圆曲线求整点功能,验证了在 d ≤ 40 ( k , d ) { ( 579 , 29 ) , ( 579 , 34 ) , ( 975 , 22 ) } E d k = 579 , 975 k d ≤ 40
但是椭圆曲线的参数 d 10 16 E d 10 16
进一步优化
回到上一节,为了求得满足
3 d ( 4 sgn ( z ) ( z 3 − k ) − d 3 ) = ◻ 的( d , z ) d ∈ [ 0 , α N ] α 2 3 − 1
为了计算满足 z 3 ≡ k mod d z d
可能的 ( d , z ) Ω ( N log N )
论文除了使用椭圆曲线排除了一部分整数 d ( d , z )
首先说一下 batch inversion,给定 k a 1 , a 2 , ⋯ a k mod n a 1 − 1 , a 2 − 1 , ⋯ , a k − 1 mod n O ( k log n )
计算 p i = a 1 a 2 ⋯ a i mod n p 1 p k k − 1
使用扩展欧几里得计算 p k − 1 O ( log n )
当i = k a i − 1 = p i − 1 p i − 1 p i − 1 − 1 = p i − 1 a i
令 p 0 = 1 i = k − 1 , k − 2 , ⋯ , 2
于是计算的时间复杂度从 O ( k log n ) O ( k + log n )
回到瓶颈一,这里将d d = p 1 e 1 p 2 e 2 ⋯ p m e m z i 3 = k mod p i
如果 p = 2 mod 3 z = k ( 2 p − 1 ) / 3 mod p O ( log p )
如果 p = 1 mod 3
令 p = 3 w m + 1 , m ∤ 3 , b = k m mod p
迭代计算 b 3 , b 3 2 , ⋯ , b 3 v b 3 v = 1 mod p v < w
任取x a = x m mod p 3 w n = log a b 3 | n a n / 3 b
取 e ∈ { 1 , 2 } 3 | ( p − e m ) z = a n e k ( p − e m ) / 3 a 3 w − 1 z , a 2 × 3 w − 1 z
然后使用hensel 提升法 扩展到 z i 3 = k mod p i e i z 3 mod d
如果先前用 batch inversion 的时候把逆元存下来,并且使用各个质数的“线性组合”来列举d d ≤ α B O ( N )
考虑瓶颈二,令
Δ = 3 d ( 4 sgn ( z ) ( z 3 − k ) − d 3 ) 选取 P = 3 ( log log N ) ( log log log N ) [ 5 , P ] M Δ p ∣ M
( Δ p ) = ( 3 d p ) ( | z | 3 − sgn ( z ) k − d 3 / 4 p ) 如果事先计算 | z | M p ∣ M N ( log log N ) ( log log log N ) O k ( N ( log log N ) ( log log log N ) )
除了复杂度的降低外,Andrew 在后续工作 Sums of three cubes 提到针对特定k k = 33 1 63.6 5.5 × 10 9 z
在具体实现方面,论文使用了 intel intrinsics 并利用超级计算机并行(10 6 d 23 k = 33
33 = 8 866 128 975 287 528 3 + ( − 8 778 405 442 862 239 ) 3 + ( − 2 736 111 468 807 040 ) 3 . 参考资料
https://baike.baidu.com/item/丢番图方程/5466939
https://zhuanlan.zhihu.com/p/354425450
Elliptic curves: number theory and cryptography
https://zhuanlan.zhihu.com/p/33853851
https://www.zhihu.com/question/267427508/answer/323883323
Transforming a general cubic elliptic curve equation to Weierstrass form
An unusual cubic representation problem
Cracking the problem with 33
Sums of three cubes (Andrew Sutherland)
https://zh.wikipedia.org/wiki/亨泽尔引理