(不定期更新)大物上笔记
大物上本质就是微积分,只不过对微分变量的选取更加讲究。
第五章
电场强度(场强)

求场强(离散型)

求场强(连续型)
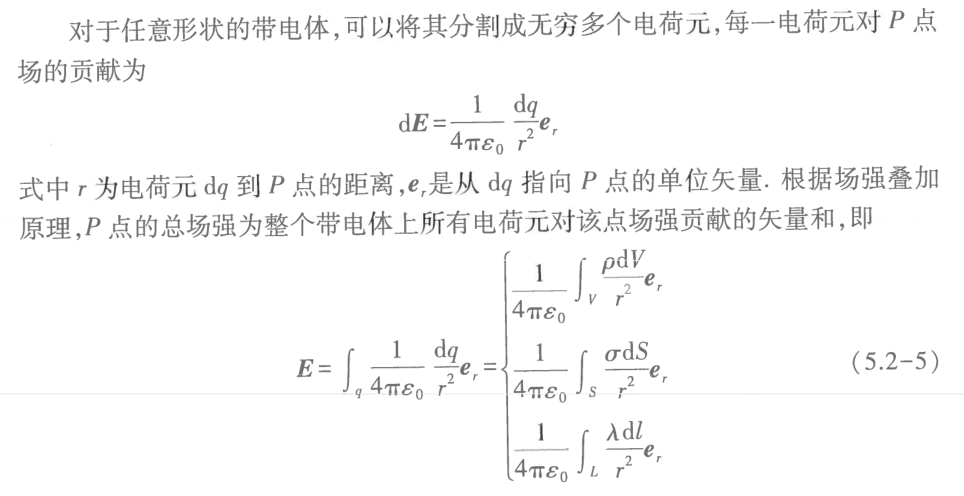
常用电场场强
点电荷、带电球壳、带电球体(外)

其中
无限长均匀带电直线(或与直线距离很近),半无限长乘1/2
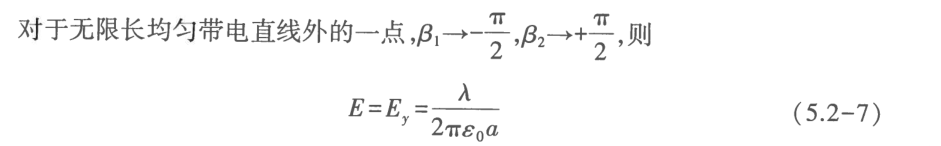
无限大均匀带电平面(或与平面距离很近)

半球壳
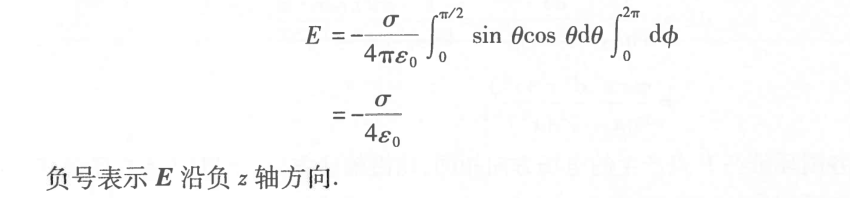
高斯定理求场强(对称性)

带电球壳


对于求球壳外的电场,可以将球壳等效为电荷集中在球心处的点电荷进行计算。
无限长柱面
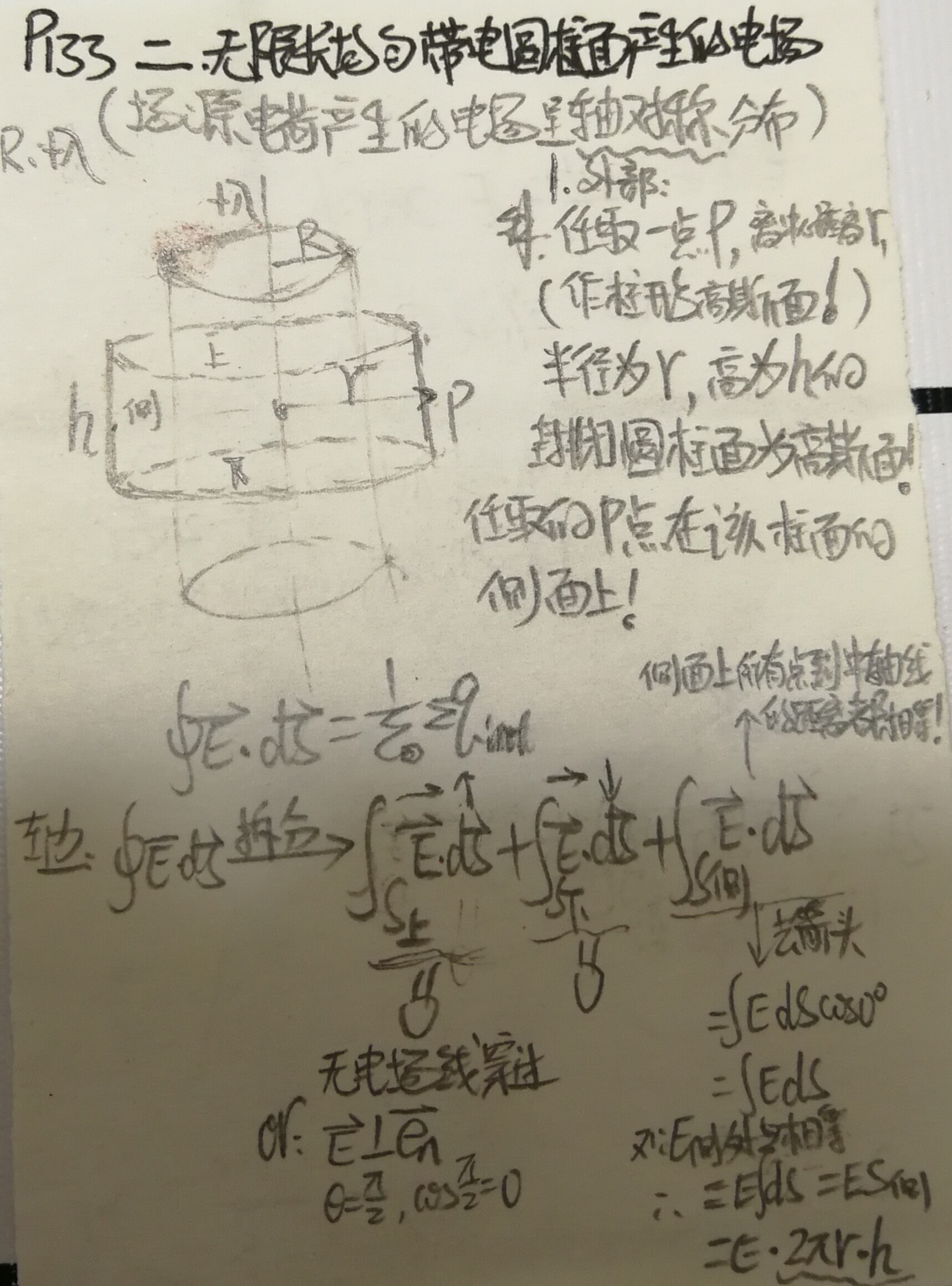

对于求柱面外的电场,可以将球壳等效为无限长均匀带电直线进行计算。

注意结果是匀强电场。一对无限大带电平面就乘2即可。
带电球体

电势
设正电荷为
电势是标量,可以直接累加.
常用电势
点电荷的电势:
连续带电体的电势分布:
带电球壳的内部电势相同(因为内部场强为0),在球壳外,电势与球心距离成反比.
带电
用电势求场强
大部分情况只考虑一元,也就是
其中大小为
第六章
导体的静电平衡
如果两个带电体相距足够远,可以看作它们电势相等。
如果物体接地,代表物体电势为0,但并不代表物体没有感应电荷。
电容和电容器
首先电容的定义式为
对于平行板电容器,有电荷面密度
对于球形电容器,设两球壳分别带电
特别地,孤立导体球的电容是
,即 趋向于正无穷的情况。
电容器串联,等效电容的倒数等于各个电容的倒数和。
电容器并联,等效电容等于各个电容的和。(与电阻相反)
静电场中的电介质
几个新物理量
引进电位移矢量
注意右侧没有
静电能计算
用电势:
用能量密度:
对于电容器:
第七章
恒定电流
电流的微分公式
电流密度
电流连续性方程
欧姆定律的微分形式
电阻的积分形式
电动势
比奥-萨法尔定律与常用磁场场强(1)
以下为了方便去掉
的箭头。
无限长载流导线
载流圆线圈轴线上一点
当
时,
长直密绕螺线管轴线上一点
当螺管无限长,
,半无限长就除以2。
安培环路定理与常用磁场场强(2)
安培环路定理(类比高斯定理):
无限长圆柱体
在圆柱内部:
在圆柱外部:
无限长直螺线管&螺绕环
根据安培环路定理,分别取圆形、矩形回路,近似处理后,均可得到:
其中
无限大载流平面
故无限大载流平面的两侧为匀强磁场。
位移电流与全电流
电荷定向移动形成的电流为传导电流
位移电流密度:
位移电流:
普遍的安培环路定理:
运动电荷在磁场中受力
洛伦兹力:
匀强磁场中的匀速圆周运动
- 螺距
霍尔效应
霍尔电势差
N型与P型的判断:(填坑)
载流导线在磁场中受力
非闭合型:
闭合型(圆形、矩形):
- 磁矩:
- 磁力矩:
(难点在于方向判断)
磁介质
绕核旋转的电子有两个磁矩,一个是“公转”的轨道磁矩,一个是“自转”的自旋磁矩,前者大于后者。
以轨道磁矩为例,可等效为环形电流
引入磁场强度
几个新物理量(以下省略方向):磁场强度
第八章
法拉第电磁感应定律
负号用楞次定律解释(来拒去留)
感应电流
感应电荷
动生电动势
电动机:
法拉第圆盘电动机:
感生电动势
法拉第实验公式:
麦克斯韦理论公式:
变化的磁场激发电场:
自感与互感
- 都是先找磁通量的表达式
- 电流前面的系数就是
或者 - 磁通量对时间的一阶导数就是
或者
自感
互感
能量
能量密度
总能量
对RL回路:
(电源的总能量=自感获得的能量+电阻消耗的能量)
麦克斯韦方程组
其中




















