（转载）凑8游戏——图论分析

发表于 更新于 分类于 阅读次数： 3 本文字数： 6.6k 阅读时长 ≈ 6 分钟

凑8游戏由 Max，也就是创办这个网站的人，于初一军训期间介绍给笔者。规则如下：

开局时，两个人两只手都是1，双方轮流，每轮玩家可以将自己手上的一个数字的值变为该数字和对方手上某个数字的和（只准加，不准加自己），如果超过7，一律变为1，如果为8，则撤手，两只手都撤下为赢。

此游戏有无数变种（正因此随机找一个人很有可能因不认同规则而玩不起来），但 Max 的变种最吸引笔者，因为可以靠自己变7乃至双7限制对方的选择，给纯粹随波逐流的游戏增添了策略。高中时，笔者就试图分析此游戏的策略，无奈学艺不精，半途而废。4年后，笔者受室友影响，沉迷上了国际象棋，对求解器的原理颇好奇，于是一鼓作气，将其解出。

笔者目前的编程功底不能说比往年高了多少，至今仍然几乎是高一用 Python 刷洛谷攒下的功底，换任何一门语言都不能习惯——即使是类型系统严谨很多的 Rust 和目前最熟悉的 TypeScript。能写出来，也许要感谢 ChatGPT 和 Copilot 吧。

本文写给无博弈论基础者。

初步分析

策梅洛定理（英语：Zermelo's theorem）是博弈论的一条定理，以德国数学家恩斯特·策梅洛命名。定理表示在二人的有限游戏中，如果双方皆拥有完全的信息，并且运气因素并不牵涉在游戏中，那先行或后行者当中必有一方有必胜/必不败的策略。

-- Wikipedia

本游戏信息完全公开，不牵涉运气，可惜循环是经常能遇到的局面，不能直接适用策梅洛定理。不过笔者分析时，直接把循环视为“双方必不败”的一种，仍然得到了看似正确的结论。

我们就从此猜想开始吧：要么先手方有必胜策略，要么后手方有必胜策略，要么循环。

表示状态

1
2
3
4
OneHand: TypeAlias = Tuple[int | None, int | None]
# False 表示轮到 state[0]，True 则为 state[1]
Turn: TypeAlias = bool
State: TypeAlias = Tuple[OneHand, OneHand, Turn]

此游戏状态相当有限，每只手可以是 1-7 或者撤回，而且顺序不影响，故两只手的状态为 。表示完整局面时，我把相同的数字状态、但两人先手后手不同的局面视为不同局面，因为：

  • 这样画决策树时，可以清晰表示黑白两色交替行动；
  • 双方能打出的局面并不对称，比如游戏永远无法回到 ((1, 1), (1, 1))，这样的局面只有先手方能遇到。

故，潜在状态有 种。

遍历可能状态

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
StartIndex: TypeAlias = int
EndIndex: TypeAlias = int

graph: List[Tuple[StartIndex, EndIndex]] = []
traversed: set[int] = set()
to_be_traversed: set[int] = set()

# 广度优先遍历
# 起点为 game_all_possible[0]
to_be_traversed.add(0)
while to_be_traversed:
    current_index = to_be_traversed.pop()
    traversed.add(current_index)
    current_state = game_all_possible[current_index]
    for next_state in get_next_states(current_state):
        next_index = game_all_possible_reverse_dict[next_state]
        graph.append((current_index, next_index))
        if next_index not in traversed:
            to_be_traversed.add(next_index)

这样，从起点出发，我们得到了能打出的所有局面——1934种。

我们看一看有哪些局面是存在/缺失的：

平凡的情况

以下情况平凡地不存在：

  • 终局时，轮到两只手都撤下的一方。
  • 两人都撤下双手。

终局

终局仅有46种可能，双方对称：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 存在的组
((1, 1), (None, None), False)           ((None, None), (1, 1), True)
((1, 2), (None, None), False)           ((None, None), (1, 2), True)
((1, 3), (None, None), False)           ((None, None), (1, 3), True)
((1, 4), (None, None), False)           ((None, None), (1, 4), True)
((1, 5), (None, None), False)           ((None, None), (1, 5), True)
((2, 5), (None, None), False)           ((None, None), (2, 5), True)
((3, 5), (None, None), False)           ((None, None), (3, 5), True)
((4, 5), (None, None), False)           ((None, None), (4, 5), True)
((5, 5), (None, None), False)           ((None, None), (5, 5), True)
((1, 6), (None, None), False)           ((None, None), (1, 6), True)
((3, 6), (None, None), False)           ((None, None), (3, 6), True)
((5, 6), (None, None), False)           ((None, None), (5, 6), True)
((1, 7), (None, None), False)           ((None, None), (1, 7), True)
((2, 7), (None, None), False)           ((None, None), (2, 7), True)
((3, 7), (None, None), False)           ((None, None), (3, 7), True)
((4, 7), (None, None), False)           ((None, None), (4, 7), True)
((5, 7), (None, None), False)           ((None, None), (5, 7), True)
((6, 7), (None, None), False)           ((None, None), (6, 7), True)
((7, 7), (None, None), False)           ((None, None), (7, 7), True)
((1, None), (None, None), False)        ((None, None), (1, None), True)
((3, None), (None, None), False)        ((None, None), (3, None), True)
((5, None), (None, None), False)        ((None, None), (5, None), True)
((7, None), (None, None), False)        ((None, None), (7, None), True)

缺失的情况不好解释，因为逆着推几步，不会很快得到矛盾。

（Max 能来试试吗？）

很遗憾，暂时没有什么从数学角度找到解决问题的灵感。如果 BFS 都搜不到，那就当作证明了情况不存在吧。

标记状态胜负

较小的数字组

为了更加方便观察该问题，我们可以先尝试凑“3”的一个例子，这样节点总数不会太多，因此可以画出状态转移图：

  • 这里正方形表示起始状态，圆表示中间状态，star 表示终局状态。
  • 白色表示先手轮，黑色表示后手轮。

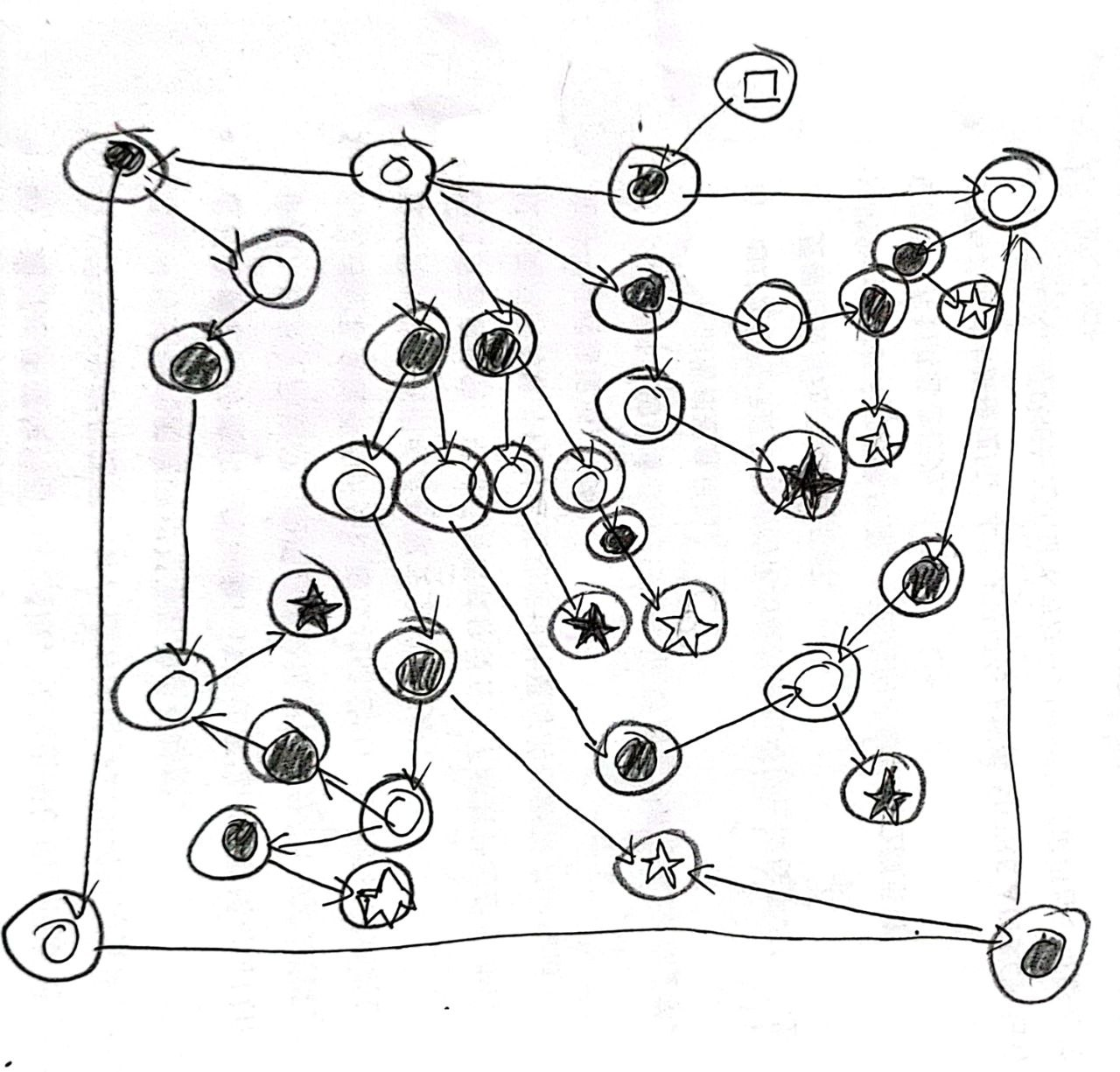
下一步 Max 选择了拓扑排序。下面简要说一下拓扑排序的处理方法（详细过程可见 oi-wiki 相关内容）：

  1. 首先把这个图的所有边反向，存储每个点的入度数量，这样所有的终局节点便成了全部入度为0的点，把这些点都放进队列里。
  2. 对于队列开头的点，列举其连接的所有边指向的点，并将这些指向的点的入度数量减1。如果指向的点入度数量为0，便将该点放进队列。列举完成后从队列中删除该点。
  3. 重复 (2) 的过程直到队列为空，删除点的序列便是正确的拓扑排序。

然后我们可以通过策梅洛定理，从胜负已知的终局状态出发，如此标记每种状态：

  • 如果存在下一步使对手必败，则本步必胜；
  • 否则，如果存在下一步能打平，则本步能打平；（该游戏不适用）
  • 如果所有下一步对手都必胜，则本步必败。

进行手推之后，我们可以得到如下图的结果：

  • 边框亮绿表示轮次方大赢（即轮次方撤走了两只手而后手方没有撤走一只），浅绿表示小赢，红色表示小输，粉色表示大输。

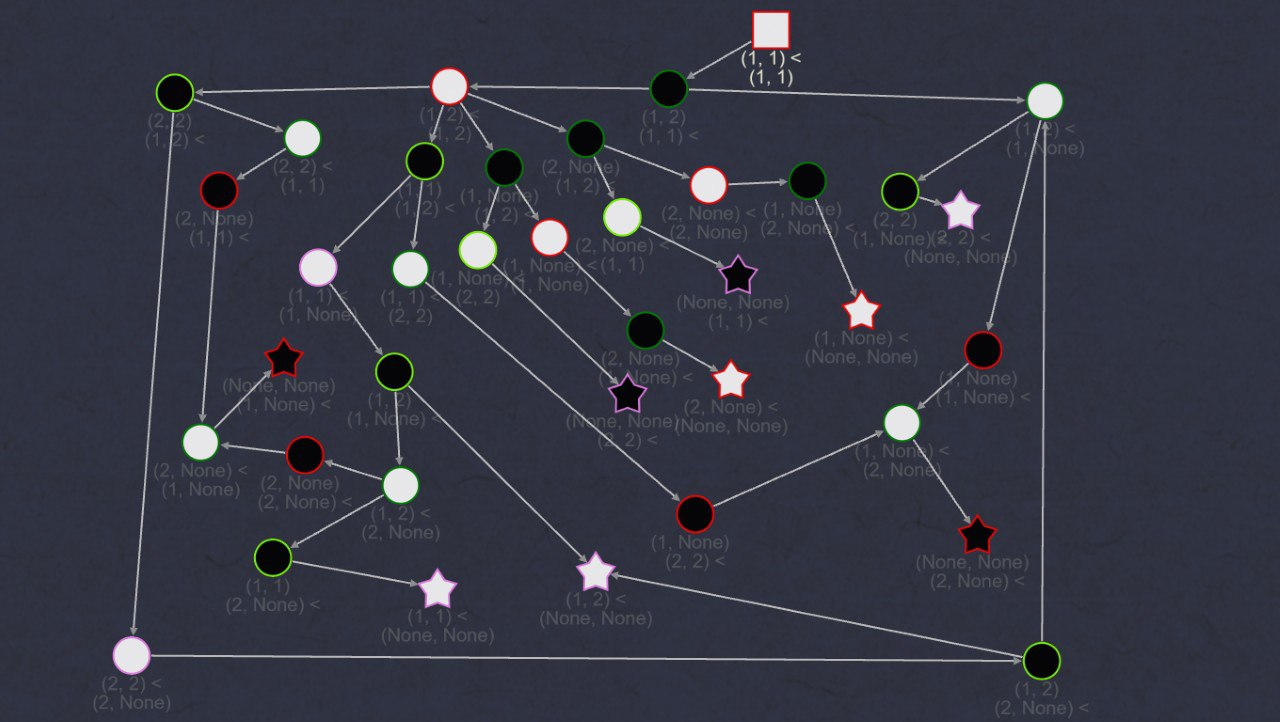
可以观察到，在凑“3”游戏中，先手方是必输的。

凑“8”的情况

凑“8”的情况与凑“3”类似，但我这里选择了进行反复迭代以解决拓扑排序不能处理带环图的限制，状态转移方程与策梅洛定理相同。这里由于状态数较多，因此选择了代码实现，思路如下：

因为状态有限，我们可以标记上每种状态，同时也就得出了最佳游戏策略。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# 标记终局
for state in game_all_possible_traversible:
    if len(get_next_states(state)) == 0:
        (a, b), (c, d), e = state
        if [a, b, c, d].count(None) == 2:
            retrograde_dict[state] = -2
        else:
            retrograde_dict[state] = -1

# 必赢或者必输的父节点
while True:
    print(retrograde_dict.__len__())

    not_changed = True
    for state in game_all_possible_traversible:
        state_index = game_all_possible_reverse_dict[state]
        if retrograde_dict.get(state, None) in [-2, -1, 1, 2]:
            parents_indexes = reversed_graph[state_index]
            for parent_index in parents_indexes:
                parent_state = game_all_possible[parent_index]
                # 如果已经算过此 parent，则跳过
                if retrograde_dict.get(parent_state, None) is not None:
                    continue
                childs_indexes = forward_graph[parent_index]
                # 如果 parent 的所有子节点均为大赢，则 parent 大输
                if all(
                    retrograde_dict.get(game_all_possible[child_index], None) == 2
                    for child_index in childs_indexes
                ):
                    retrograde_dict[parent_state] = -2
                    not_changed = False
                # 如果 parent 的所有子节点均为赢，则 parent 输
                elif all(
                    retrograde_dict.get(game_all_possible[child_index], None) in [1, 2]
                    for child_index in childs_indexes
                ):
                    retrograde_dict[parent_state] = -1
                    not_changed = False
                # 如果存在子节点为大输，则 parent 大赢
                elif any(
                    retrograde_dict.get(game_all_possible[child_index], None) == -2
                    for child_index in childs_indexes
                ):
                    retrograde_dict[parent_state] = 2
                    not_changed = False
                # 如果存在子节点为输，则 parent 赢
                elif any(
                    retrograde_dict.get(game_all_possible[child_index], None)
                    in [-1, -2]
                    for child_index in childs_indexes
                ):
                    retrograde_dict[parent_state] = 1
                    not_changed = False
    if not_changed:
        break

据说传统的策梅洛定理不能处理循环情况，但我没做任何特殊处理就解决了，不知道为什么。

据此，我们得出所有节点的情况：

1
2
3
4
5
130 -2
392 -1
680 1
264 2
468 None

其中正赢负输，None 为不确定，在此游戏不存在平局的情况下，None 为循环。2表示赢时对方没有撤下一只手，1表示已经撤下一只：看起来大赢没这么容易。

综上所述，1466种状态具有确定的胜负，剩下468种状态（包括开局）不确定，构成连通图且成环，故此游戏双方皆有必不败策略。后手方第一步可以选择 1 2 或者 1 3。我暂时没有证据哪种更好（虽然自己偏爱 1 3），只知道无论哪种，先手方第二步都有1/4的情形暴毙。

推广到其他情况

先说结论：

  • 是先手胜利。
  • 是后手胜利。
  • 时确定是最优策略下游戏没有胜负。
  • 当 ，Max 和我都猜想因为图中有环导致最优策略下游戏没有胜负，但并没能够证明它。

有缘人可以来试试，这是个有趣的问题。

顺便指出一点，图中有环并不是最优策略下游戏没有胜负的充分条件，除了的情况之外，这里也可以轻松举出一个反例：

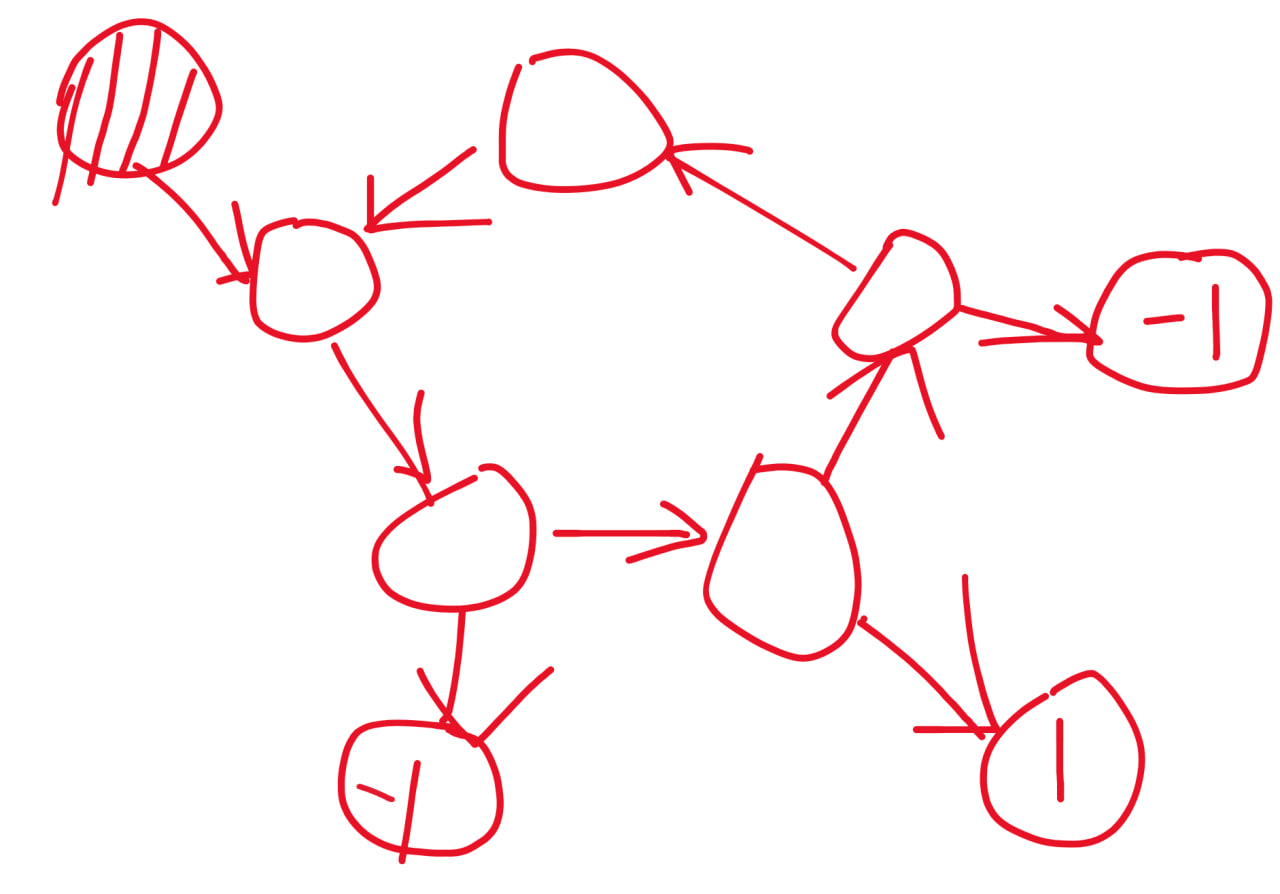
如果这里 1 表示当前轮次方胜利，-1 表示当前轮次方失败，这个游戏是先手必胜的。（虽然实际建图不会出现环周长为奇数的情况，但这个图已经可以说明问题）

Alice 先将棋子从阴影点移动到环的入口，Bob 没有选择只能沿着环走一步。此时 Alice 可以继续沿着环走一步，也可以选择走向“-1”处。聪明的 Alice 当然会选择后者，这样棋子就位于 -1 处了。此时轮到 Bob，他作为当前轮次方并且节点值为 -1，因此 Bob 负，Alice 胜。

所以严格来说，这其实是两个问题：

  1. 在 的情况下，图中必有环。（必要条件）
  2. 如果 (1) 成立，证明不会出现上述反例的情况。

随后对感兴趣的读者说一下 的具体结果：

思路还是建图+策梅洛定理的状态转移+反复迭代（或拓扑排序）。类似于上一节，这里给出所有节点的胜负情况，并做成一个表。

-2（大输） -1（小输） 1（小赢） 2（大赢） None（无胜负） 最终结果（先手）
2 0 0 4 0 - 胜
3 7 12 11 8 - 负
4 22 43 51 32 - 胜
5 42 99 139 66 - 负
6 66 193 279 122 - 负
7 112 349 522 213 - 胜
8 130 392 680 264 468 -
9 179 670 1223 378 574 负

迷信分析

我当年玩时有诸多经验法则。最著名的是“3的吉利性”，狭义指如果自己有3而且对方碰出双7，则自己把3留下另一只手变1，即可赢。广义就是字面意思。我马上就能知道这有没有道理了……

结论：有道理！ 2, 3 < 7, 7 3, 3 < 7, 7 是不可能的局面。 1, 3 < 7, 7 输。其余情况留住3就能赢。

其余情况，4吉利，2未知，5 6 7凶险。 如果自己一只手是1，那么另一只手1 2 5 7能赢，3 4 6输。

——

ycy 创造过某种定式： 1, 7 < ycy 2, 6 ycy 赌我不敢碰出7让他下，于是： 1, 1 2, 6 < UNKNOWN

1, 1 < UNKNOWN 3, 6

1, 7 3, 6 < UNKNOWN

1, 7 < UNKNOWN 4, 6

1, 1 4, 6 < WIN

1, 1 < WIN 5, 6

1, 7 5, 6 < LOSE

1, 7 < WIN 6, 6

1, 1 6, 6 < LOSE

循环半天，仍然没躲过需要先送走对方的命运。ycy 已经忍俊不禁，我一口气输掉之后则更灿烂了。然而，循环开始他本可以直接赢！中途跳车我也有机会赢！

参见

项目仓库地址：https://github.com/Master-Hash/eight

Python 脚本：main.py

演示网站：https://land.hash.memorial/count8?c=3

这里 的取值范围是 .