multimod_fast 真的是对的吗？

发表于 2024-03-20 分类于笔记本文字数： 9.9k 阅读时长 ≈ 9 分钟

事情要从这段代码说起：

// gcc test.c -o test -fwrapv
int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}

昨天晚上，有人给我发了这段据说可以替代快速乘的代码，让我解释这段代码的正确性。这段代码可以把时间复杂度从降到。显然，我们都知道int64_t与double之间的强制转换会丢失精度，因此我对这段代码的正确性产生了怀疑。

preliminaries

首先，我们得知道浮点数在C语言中的表示。IEEE 754标准规定了浮点数的表示方法，其中double类型的浮点数占用64位，其中1位是符号位，11位是指数位，剩下的52位是尾数位。我们可以参考这篇文章来了解更多关于浮点数的知识，我这里就不赘述了。

然后，我们得知道-fwrapv编译选项的作用。根据gcc的官方文档，-fwrapv选项的作用是：当有符号整数溢出时，结果是对2的补码取模。这意味着，当有符号整数溢出时，结果会被截断为一个合法的值。例如，INT_MAX + 1的结果是INT_MIN。

error analysis

(double)a

根据前置知识中学到的内容可以推断，64位浮点数的相对精度为（为什么？）。那么，理论上int64_t强转double的话的绝对精度会是多少呢？我们可以使用简单的数学推导来得到答案。

我们知道，int64_t的范围是，因此，最大的绝对精度可以粗略地估计为。这意味着，int64_t强转double的话，最大的绝对误差大约是。

接下来，我们可以尝试构造一个测试用例来验证这个结论：

#include <stdio.h>
#include <stdint.h>
#include <math.h>

int64_t a = 9223372036854775807;
double b;


int equal(double x, double y) {
  return fabs(x - y) < 0.0000001;
}

int judge(int64_t offset) {
  double c = (double)(a - offset);
  return equal(c, b);
}

int64_t bisect(int64_t low, int64_t high) {
  if (low == high) {
    return low - 1;
  }
  int64_t mid = (low + high) / 2;
  if (judge(mid)) {
    return bisect(mid + 1, high);
  } else {
    return bisect(low, mid);
  }
}

int main() {
  b = (double)a;
  printf("%ld\n", bisect(1, 1000000000));
  double c = (double)(a - 512);
  printf("%lf %lf\n", b, c);
  //printf("%d\n", equal(b, c));
  //printf("%d\n", judge(200000000));
  return 0;
}

实际测试告诉我们，当a = INT64_MIN时，二分的合法区间offset为；当a = INT64_MAX时，二分的合法区间offset为，合起来的取值范围就是。如果超过这个合法区间，转换double值就从跳变到，刚好差了,也就是。

(double)a * b

asm

我们先分析一个double是如何和int64_t相乘的，看一段简单的代码：

int main() {
  int64_t a = 3;
  int64_t b = 4;
  double c = (double)a * b;
  return 0;
}

在 x86_64 环境下的反汇编如下：

0000000000001119 <main>:
    1119:       55                      push   rbp
    111a:       48 89 e5                mov    rbp,rsp
    111d:       48 c7 45 e8 03 00 00    mov    QWORD PTR [rbp-0x18],0x3
    1124:       00 
    1125:       48 c7 45 f0 04 00 00    mov    QWORD PTR [rbp-0x10],0x4
    112c:       00 
    112d:       66 0f ef c9             pxor   xmm1,xmm1
    1131:       f2 48 0f 2a 4d e8       cvtsi2sd xmm1,QWORD PTR [rbp-0x18]
    1137:       66 0f ef c0             pxor   xmm0,xmm0
    113b:       f2 48 0f 2a 45 f0       cvtsi2sd xmm0,QWORD PTR [rbp-0x10]
    1141:       f2 0f 59 c1             mulsd  xmm0,xmm1
    1145:       f2 0f 11 45 f8          movsd  QWORD PTR [rbp-0x8],xmm0
    114a:       b8 00 00 00 00          mov    eax,0x0
    114f:       5d                      pop    rbp
    1150:       c3                      ret

显然，并不是所有人都知道pxor,cvtsi2sd,mulsd和movsd指令的含义，这里我们得翻一下 intel 的 manual：

pxor：对浮点寄存器（xmm?）的异或操作。
cvtsi2sd：将int64_t 转成 double，存到浮点寄存器。
mulsd：double 与 double 乘，存在第一个（目的）操作数。
movsd：将源操作数复制给目的操作数。

我们在gdb中b 0x114a，然后continue，断下来后xmm0的状态如下：

(gdb) p $xmm0
$4 = {v8_bfloat16 = {0, 0, 0, 2.625, 0, 0, 0, 0}, v8_half = {0, 0, 0, 2.0781, 0, 0, 
    0, 0}, v4_float = {0, 2.625, 0, 0}, v2_double = {12, 0}, v16_int8 = {0, 0, 0, 0, 
    0, 0, 40, 64, 0, 0, 0, 0, 0, 0, 0, 0}, v8_int16 = {0, 0, 0, 16424, 0, 0, 0, 0}, 
  v4_int32 = {0, 1076363264, 0, 0}, v2_int64 = {4622945017495814144, 0}, 
  uint128 = 4622945017495814144}

上网查询相关数据得知，double 的 4622945017495814144 转回 int64_t 就是正确的结果12。

actual analysis

从上文可以得知，(double)a * b 的计算方法是将a和b同时转换成浮点形式，然后再执行mulsd指令。

接下来，我们来分析(double)a * b的结果。我们已经知道，int64_t强转double的话，乘数的误差范围为。这里由于IEEE 754浮点乘原理较为复杂，这里我打算直接以先前累积的算术误差来估计。

对于最大值而言：

对于最小值而言:

我们来再写份代码验证自己的猜想是否正确：

#include <stdio.h>
#include <stdint.h>
#include <math.h>

int64_t a = -9223372036854775808;
double b;


int equal(double x, double y) {
  printf("fabs(%lf - %lf) = %lf\n", x, y, fabs(x - y));
  return fabs(x - y) < 0.0000001;
}

int judge(int64_t offset) {
  double c = (double)(a + offset)*(a + offset);
  // should be (double)(a + offset)*(-a + offset) when getting the minimum
  return equal(c, b);
}

int64_t bisect(int64_t low, int64_t high) {
  if (low == high) {
    return low - 1;
  }
  int64_t mid = (low + high) / 2;
  if (judge(mid)) {
    return bisect(mid + 1, high);
  } else {
    return bisect(low, mid);
  }
}

int main() {
  // the "b" in context is another a in next line of code, 
  // instead of the result on the left
  // should be (double)a*(-a) when getting the minimum
  b = (double)a*a;
  printf("%ld\n", bisect(1, 1000000000));
  //double c = (double)(a - 512);
  //printf("%lf %lf\n", b, c);
  //printf("%d\n", equal(b, c));
  //printf("%d\n", judge(200000000));
  return 0;
}

验证结果表明，和的合法取值范围没有变化，当a = b = INT64_MIN，offset = 512时，我们可以求得绝对误差最大值为，也就是；同理，当a = INT64_MAX, b = -INT64_MAX，offset = -511时，我们可以求得绝对误差最小值为。

综上，我们得到先前的推测比实际绝对误差少了一半左右，还是可以接受的。

(double)a * b / m

除法的话比较玄学。根据相对误差公式，若，则有：

和有较为简单的正相关关系，因此为了取极值，还是取，因此。

的话，因为浮点运算的特性，在之前恒为，在这个区间会跳变为。我们稍微对式子变形一下：

我们可以发现，总体上是一个减函数，只在处不单调。而显然的极值不会出现在处，因此我们可以确定，仍然是时，商的绝对误差最大。

代入回原来的式子(double)a * b / m，可以确认当a = b = INT64_MIN, m = 1时，和a = b = INT64_MIN, m = -1时，求得的绝对误差范围为。

(int64_t)((double)a * b / m) * m

先前(double)a * b / m的绝对误差已经大于int64_t本身的范围了，所以理论来说转成int64_t之后最坏情况下没有任何精度。

因此，从数学的角度而言，这个函数不是恒成立的。已经没有什么接着分析下去的必要了。

when it will satisfy

那我们接着来看看，分别在什么数量级上，(int64_t)((double)a * b / m) * m这个式子会能被整除。

import random
import subprocess

matrix = [[1 for _ in range(62)] for _ in range(62)]


# try this multiple times to reduce the chance of false positive   
for _ in range (10):

    A = []
    B = []
    C = []

    for i in range(0, 62):
        A.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        B.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        C.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    lenA = len(A)
    lenC = len(C)


    for i in range(lenA):
        for j in range(lenC):
            command = ["./test", str(A[i]), str(B[i]), str(C[j])]
            result = subprocess.run(command, stdout=subprocess.PIPE)
            output = int(result.stdout.strip())
            if output % C[j] != 0:
                matrix[i][j] = 0 # invalid

import numpy as np
import matplotlib.pyplot as plt

colored_matrix = np.array(matrix)
plt.imshow(colored_matrix, cmap='Blues', interpolation='nearest')
plt.show()

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <math.h>


double f(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

double g(int64_t x, int64_t y, int64_t z) {
  return (double)x * y / z;
}

int64_t h(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}


int main(int argc, char *argv[]) {
  if (argc != 4) {
    return 1;
  }

  int64_t a = atol(argv[1]);
  int64_t b = atol(argv[2]);
  int64_t c = atol(argv[3]);

  printf("%ld\n", h(a, b, c));
  return 0;
}

绘图结果如下（横轴为，纵轴为与，蓝色为结果正确）。可以发现，当或者时，结果才是正确的。

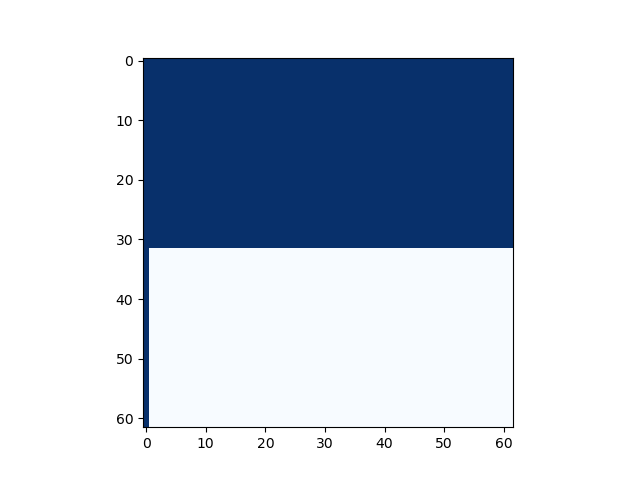
我们再略微修改一下代码，理论上讲，如果(int64_t)((double)a * b / m) * m是的倍数，那么(a * b - (int64_t)((double)a * b / m) * m) % m本身应该可以化简为(a * b) % m。也就是整个multimod_fast成立与上一个命题等价，画出来的图也应该是一致的：

import random
import subprocess

matrix = [[1 for _ in range(62)] for _ in range(62)]


# try this multiple times to reduce the chance of false positive   
for _ in range (10):

    A = []
    B = []
    C = []

    for i in range(0, 62):
        A.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        B.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    for i in range(0, 62):
        C.append(2**i + random.randint(max(-2**i+1, -10), min(2**i-1, 10)))

    lenA = len(A)
    lenC = len(C)


    for i in range(lenA):
        for j in range(lenC):
            command = ["./test", str(A[i]), str(B[i]), str(C[j])]
            result = subprocess.run(command, stdout=subprocess.PIPE)
            output = int(result.stdout.strip())
            if output != A[i] * B[i] % C[j]:
                matrix[i][j] = 0 # invalid

import numpy as np
import matplotlib.pyplot as plt

colored_matrix = np.array(matrix)
plt.imshow(colored_matrix, cmap='Blues', interpolation='nearest')
plt.show()

#include <stdio.h>
#include <stdint.h>
#include <stdlib.h>
#include <math.h>


double f(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

double g(int64_t x, int64_t y, int64_t z) {
  return (double)x * y / z;
}

int64_t h(int64_t x, int64_t y, int64_t z) {
  return (int64_t)((double)x * y / z) * z;
}

int64_t multimod_fast(int64_t a, int64_t b, int64_t m) {
    int64_t t = (a * b - (int64_t)((double)a * b / m) * m) % m;
    return t < 0 ? t + m : t;
}


int main(int argc, char *argv[]) {
  if (argc != 4) {
    return 1;
  }

  int64_t a = atol(argv[1]);
  int64_t b = atol(argv[2]);
  int64_t c = atol(argv[3]);

  printf("%ld\n", multimod_fast(a, b, c));
  return 0;
}

然而，实际上的图长这样。我们发现之前那个式子是一个充分条件，并不等价。同时，当后，越大，符合条件的也就越多，这也符合我们的直觉。

我们也可以举一个实实在在的反例：。multimod_fast的结果是，但正确结果是，看一下图大该也落在了图中的白色区域。

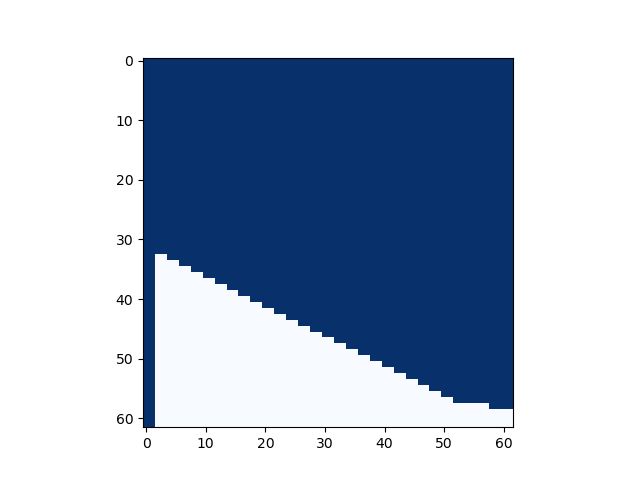
总的来说，我们至少可以说明当时，这个式子是恒成立的了，接下来让我们尝试证明它。

proof

我们先前说过“(int64_t)((double)a * b / m) * m是的倍数”是这个函数返回正确结果的充分条件，因此我们只需证明(int64_t)((double)a * b / m) * m在时该式是的倍数这个条件即可。

有些人可能会有疑问，(int64_t)((double)a * b / m)肯定是一个整数，那现在欲证的式子肯定是的倍数啊。其实这些人忽略了一个问题：64位的整数有符号溢出。即使我们开启了-fwrapv选项，如果，那么这个欲证式子在溢出之后仍然不会是的倍数。

因此，只要本身不溢出,那么(int64_t)((double)a * b / m) * m就一定是的倍数。而是上式的充分条件（更硬的结论是），multimod_fast就能正确实现它的功能，跟浮点误差没有任何关系。

summary

multimod_fast 这个式子仅在本身不溢出int64_t的情况是正确的，它无法完全替代均为int64_t的的快速乘。